相加平均≧相乗平均≧調和平均を裏技を使って証明します。どうも,ユキです。目にもとまらぬ速さで証明するので,まばたき禁止ですwww
この記事を読む前に,手元に目薬でも用意しておいてください。
この記事を読むメリット
・相加平均≧相乗平均≧調和平均の関係を視覚的に理解できるようになる
・相加平均,相乗平均,調和平均の等号成立条件も容易に出てくる。
相加平均,相乗平均,調和平均ってなんだっけ?
相加平均\(\overline{x}\)
$$\overline{x}=\frac{1}{n}(x_1+x_2+\cdots+x_n) $$
相乗平均\(\overline{x}^G\)
$$\overline{x}^G=(x_1x_2\cdots x_n)^{\frac{1}{n}}$$
調和平均\(\overline{x}^H\)
$$\overline{x}^H=\frac{1}{\frac{1}{n}(\frac{1}{x_1}+\frac{1}{x_2}+\cdots+\frac{1}{x_n})}$$
でした。詳しくは,前の記事で解説しています。
相加平均相乗平均の進化形
相加平均と相乗平均の関係は,高校で習うと思います。式で書くと
\(\frac{1}{2}(x_1+x_2)\geq \sqrt{x_1x_2}\)
実は,この不等式には続きがあります。
\(\frac{1}{2}(x_1+x_2)\geq \sqrt{x_1x_2}\geq \frac{1}{\frac{1}{2}(\frac{1}{x_1}+\frac{1}{x_2})}\tag{1}\)
です。
この式を見るとわかるとおり,相加平均は相乗平均より大きく,調和平均は相乗平均より小さいです。
普通の証明
証明したいのは,式(1)の不等式です。
\(\frac{1}{2}(x_1+x_2)\geq \sqrt{x_1x_2}\geq \frac{1}{\frac{1}{2}(\frac{1}{x_1}+\frac{1}{x_2})}\tag{1}\)
式(1)のような,3つの不等式をいっぺんに証明するのは骨が折れるので,
$$\frac{1}{2}(x_1+x_2)\geq \sqrt{x_1x_2}\tag{2}$$
$$\sqrt{x_1x_2}\geq \frac{1}{\frac{1}{2}\frac{1}{x_1}+\frac{1}{x_2}}\tag{3}$$
不等式(1)を式(2),式(3)に分解しました。式(2)と式(3)をそれぞれ証明していきます。
相加平均相乗平均の関係証明
\((x_1-x_2)^2\geq 0\)
\(x_1^2-2x_1x_2+x_2^2\geq 0\)
ここで,両辺に\(4x_1x_2\)を足すと,
\(x_1^2+2x_1x_2+x_2^2\geq 4x_1x_2\)
\((\frac{1}{2}(x_1+x_2))^2\geq x_1x_2\)
よって,
\(\frac{1}{2}(x_1+x_2)\geq \sqrt{x_1x_2}\)
となり,式(2)は示されます。
相乗平均と調和平均の関係証明
\((\frac{1}{x_1}-\frac{1}{x_2})^2 \geq 0)
\((\frac{1}{x_1})^{2}-2\frac{1}{x_1}\frac{1}{x_2}+(\frac{1}{x_2})^{2}\geq 0\)
ここで,両辺に\(4\frac{1}{x_1}\frac{1}{x_2}\)を足すと,
\(\frac{1}{x_1})^2+2\frac{1}{x_1}\frac{1}{x_2}+(\frac{1}{x_2})^2\geq 4\frac{1}{x_1}\frac{1}{x_2}\)
\((\frac{1}{x_1}+\frac{1}{x_2})^2 \geq 4\frac{1}{x_1x_2}\)
\(x_1x_2 \geq \frac{4}{(\frac{1}{x_1}+\frac{1}{x_2})^2}\)
\(\sqrt{x_1x_2} \geq \frac{2}{\frac{1}{x_1}+\frac{1}{x_2}}\)
よって,
\(\sqrt{x_1x_2} \geq \frac{1}{\frac{1}{2}(\frac{1}{x_1}+\frac{1}{x_2})}\)
となり,式(3)は示されます。<終>
式(2)と式(3)が示されたので,
\(\frac{1}{2}(x_1+x_2)\sqrt{x_1}{x_2}\geq \frac{1}{\frac{1}{2}(\frac{1}{x_1}+\frac{1}{x_2})}\)
式(1)が示されます。
裏技で証明
式(1)を先ほどよりも,速く視覚的に証明します。
まず,円とその直径を書き,直径上に中心と,点Aを適当にとって,長さをそれぞれ\(x_1\),\(x_2\)とします。
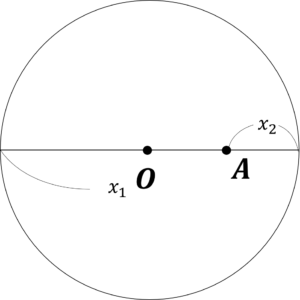
図1.円の直径上に点\(A\)をとる
次に,下図に指し示しているように,点\(B\),点\(C\)をとってあげると,図は以下のようになります。
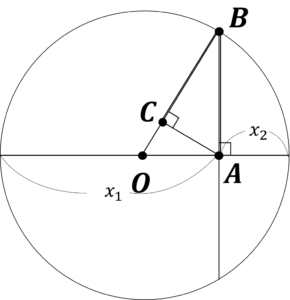
図2.相加平均相乗平均調和平均を導くための図
そうすると,図から次式が成立することが見て取れます。
\(OB\geq AB \geq BC\)
ここで,\(OB\)は相加平均,\(AB\)は相乗平均,\(BC\)は調和平均を表すので,
不等式
$$\frac{1}{2}(x_1+x_2)\geq \sqrt{x_1x_2}\geq \frac{1}{\frac{1}{2}(\frac{1}{x_1}+\frac{1}{x_2})}$$
が成立します。
<終>
この証明を見たあなたは,おそらく3つの疑問を抱いたでしょう。式で書くと,
$$OB=\frac{1}{2}(x_1+x_2)\tag{4}$$
$$AB=\sqrt{x_1x_2}\tag{5}$$
$$BC=\frac{1}{\frac{1}{2}(\frac{1}{x_1}+\frac{1}{x_2})}\tag{6}$$
式(4)の導出
\(円の半径=\frac{1}{2}円の直径\)
ここで,\(円の半径=OB\)です。そして,\(円の直径=x_1+x_2\)で表されます。ということは,
$$OB=\frac{1}{2}(x_1+x_2)$$
となり,式(4)は成立します。
式(5)の証明
方べきの定理を使います。\(AB\)は,円の直径によって垂直二等分されているので,
\(AB・AB=x_1・x_2\)
です。よって,\(AB\)は,
\(AB=\sqrt{x_1x_2}\)
となり,式(5)が証明されました。
式(6)の証明
これは,三角形の相似を使うことによって導きます。
図を見ると,\(\triangle OAB\)と\(\triangle ACB\)について,三角形の二角が等しいので,\(\triangle OAB\sim ACB\)が成立します。
\(\triangle OAB\)と\(\triangle ACB\)が相似ということは,辺の長さの比が一致するので,
\(BC:AB=AB:OB\)
が成立します。式を整理すると,
\(BC=\frac{AB^2}{OB}\)
となります。ここで,式(4),式(5)を代入すると,
\(BC=\frac{x_1x_2}{\frac{1}{2}(x_1+x_2)}\)
\(BC=\frac{1}{\frac{1}{2}\frac{x_1+x_2}{x_1x_2}}\)
部分分数分解を使うと,\(BC\)は,
$$BC=\frac{1}{\frac{1}{2}(\frac{1}{x_1}+\frac{1}{x_2})}$$
なって,式(6)が成立します。
まとめ
相加平均≧相乗平均≧調和平均は,下の図から明らか。



$$\frac{1}{2}(x_1+x_2)\geq \sqrt{x_1x_2}\geq \frac{1}{\frac{1}{2}(\frac{1}{x_1}+\frac{1}{x_2})}$$
最後に
相加平均相乗平均調和平均の大小関係を視覚的に表すことによって,より強固な理解を得られたかと思います。ちなみにこの証明方法は,とある高校の教員に教えていただきました。

















