ユキ

どうも，ユキです。

晴れ男なので、ひなさん必要ありません。

今日は，新海誠さんの最新映画「天気の子」の主題歌である

RADWIMPSさんの「愛にできることはまだあるかい？」

の愛を虚数iに変えて,「iにできることはまだあるのか？」という検証を含めた虚数iの魅力を話します。

http://j-lyric.net/artist/a04ac97/l04ce5f.html

今回の記事を読むメリット

・虚数iの必要性がわかる

iって何？

虚数iは，この世に存在しない想像上の数です。

iという文字は，想像上の数(imaginaire)の頭文字をとったものです。

虚数の性質を紹介します。

虚数iの性質【これだけ】

$$i=\sqrt{-1}$$

$$i^2=-1$$

iは－1の平方根として，知られています。なので，iを2乗すると-1になります。

複素数とは

実数と虚数iを組み合わせた数のことを複素数といいます。

3＋4iや8-8iのような数のことですね。

虚数iは美しい公式【オイラーの公式】

$$e^{i\theta}=cos\theta+isin\theta$$

これは，オイラーの公式と呼ばれているものです。

指数関数が，三角関数と等式をなしていることに魅力を感じますね。

この公式は，物理屋さんや，電気工学を使っている人たちにとって，避けては通れない公式です。

指数関数は，虚数iを使うと三角関数になる

オイラーの式を少し変形します。
$$e^{i\theta}=cos\theta+isin\theta$$
$$e^{-i\theta}=cos\theta-isin\theta$$
これは$cos\theta$，$sin\theta$を未知数とした。

連立方程式となっているので，
$$cos\theta=\frac{e^{i\theta}+e^{-i\theta}}{2} $$
$$sin\theta=\frac{e^{i\theta}-e^{-i\theta}}{2i} $$
と書ける。

1のi乗は？

1を何回かけても1ということは，皆さんご周知のはず。

ですが，1のi乗は何になるのか，ということで，計算します。

$$1^i=e^{ilog(1+i2n\pi)}=e^0=1$$

1になりました。1のi乗しても1なんですね。

iは積分を簡単にする

大学に入ってからの積分は，変なところに三角関数が入ってきたり，積分範囲が無限大までいく場面がしばしば出てきます。

その問題を簡潔にするために積分経路を変更して，複素積分という複素数に渡った積分を行います。

iは微分方程式の解に出てくることがある。

微分方程式とは，方程式の中に微分が含まれる方程式のことを言います。

具体例：
$$\frac{dy}{dx}-y=0　，　\frac{d^2y}{dx^2}+2\frac{dy}{dx}+2y=0$$

上のような微分方程式の場合，$$y=Ce^{λx}$$とおくことで解くことが可能です。

因みに、答えはそれぞれ

$$y=Ce^x　　y=C_1e^{(-1+i)x}+C_2e^{(-1-i)x}$$

例題1：

$$\frac{1}{2\pi}\int_{0}^{2\pi} \frac{1}{a+bsin\theta} \,d\theta$$
この問題は，分母に三角関数があるので，$t=\frac{tan\theta}{2}$とおけば，解けそうな気がしますが，積分の範囲が0から2πまでなので，積分範囲が実数のまま積分を解くと難解なものになります。

そんなときに，iがこの問題を解決します。

例題1：解答

問題の解法としては，次の3つの手順を踏めば解けます。
1.オイラーの公式を使って，$sinθ=\frac{e^{iθ}-e^{-iθ}}{2i}$と変形する。<<大学数学オイラーの公式
2.$z=e^{iθ}$とおいて，与式をzの積分に書き換える。<<高校数学Ⅲの置換積分
3.留数定理を用いると，答えにたどり着く<<大学数学の複素関数論

(1) オイラーの公式を使って，$sin\theta=\frac{e^{iθ}-e^{-iθ}}{2i}$と変形する。

$$\frac{1}{2\pi}\int_{0}^{2\pi} \frac{1}{a+b\frac{e^{iθ}-e^{-iθ}}{2i}} \,d\theta$$

$z=e^{iθ}$について，zをθで微分する。
(2) z=e^{iθ}とおいて，与式をzの積分に書き換える$\frac{dz}{dθ}=ie^{iθ}$すなはち，$dθ=\frac{dz}{ie^{i\theta}}$，積分範囲　θ：0→2π，z：|z|=1

$$=\frac{1}{2\pi}\oint_{|z|=1}\frac{1}{a+b\frac{e^{i\theta}-e^{-i\theta}}{2i}}\times \frac{1}{ie^{i\theta}}dz$$

$$=\frac{1}{2\pi}\oint_{|z|=1}\frac{1}{az+b\frac{z^2-1}{2i}}dz$$

$$=\frac{1}{2\pi}\oint_{|z|=1}\frac{1}{2iaz+b(z^2-1)}dz$$

$$=\frac{1}{2\pi}\oint_{|z|=1}\frac{1}{bz^2+2iaz-b}dz$$

(3) 留数定理を用いると，答えにたどり着く。

$$=\frac{2}{2\pi}\times2i\pi\times Res[\frac{1}{bz^2+2iaz-b}]$$

$$=2i\times[\frac{z+ia-\sqrt{-a^2+b^2}}{bz^2+2iaz-b}]_{z=-ia+\sqrt{-a^2+b^2}}$$

$$={1}{bz^2+2iaz-b}]$$

$$=2i\times[\frac{1}{z+ia+\sqrt{-a^2+b^2}}]_{z=-ia+\sqrt{-a^2+b^2}}$$

$$=2i\times\frac{1}{2i\sqrt{a^2-b^2}}$$

$$=\frac{1}{\sqrt{a^2-b^2}}$$

ただし、(a>b)

普通に計算が面倒でした。(m_m)

虚数iを使う例

ユキ

私は工学部で、これまで学んできた中では以下の通りです。

・常微分方程式を解く

・フーリエ解析、フーリエ級数展開（通信系）

・物理学全般

・量子力学

・複素表現するとき

量子力学への虚数の貢献度は偉大ですね。

iの物理学への応用

使用例の一つを紹介します。

iは電気工学系の人や，量子力学などで用いられます。

電気工学の場合は，iは計算を簡単にするために，用いられています。

具体例として，フェーザー表示があります。

量子力学の場合は，つじつまを合わせるためにiを使っています。

(ⅰ)電子工学の場合 <<高校物理インピーダンス

電気系の人は，jを使う

電気工学では，電流iと虚数iが混同するのを避けるために，虚数をjとして使います。
下例題

例題2：

次のRＬＣ直列回路で，v=Asinωtの交流電圧がかかっているときの回路を流れる電流I
を求めよ。

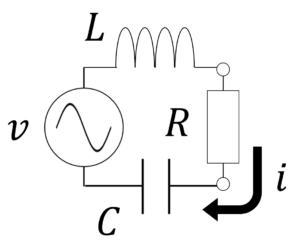
例題2：解答

電気回路の3つの素子の公式
$$v_L=L \frac{di}{dt}　V_R=Ri　i=C \frac{dv_C}{dt}$$
電圧の式
$$v=v_C+v_L+v_R$$
電圧の式に3つの素子の公式を無理矢理代入していくと，最終的に以下の式が得られます。
$$\frac{dV}{dt}=\frac{I}{C}+L \frac{d^2 I}{dt^2 }+R \frac{dI}{dt}$$

電流Ｉを求める為には，この微分を含んだ方程式を解く必要があり，面倒です。(´･д･｀)

しかし，この微分方程式は，フェーザー表示に直して解くことで，少しだけ簡単になります。
フェーザー表示
$$\frac{d}{dt}→jω$$
$$sin(ωt+φ)→\frac{e^{jφ}}{\sqrt{2}}$$
微分が邪魔なので，とすると，
$$jωV=(1/C-ω^2 L+jωR)I$$
になります。
$$I=\frac{V}{R+j(ωL-\frac{1}{ωC})}$$

$$=\frac{Ae^0}{\sqrt{2}\sqrt{R^2+(ωL-\frac{1}{ωC})^2}e^{jφ}}$$

フェーザー表示から元の式に戻すと，答えは，

$$i=\frac{Asin(ωt-φ)}{\sqrt{R^2+(ωL-\frac{1}{ωC})^2}}$$

$$(∵tanφ=\frac{ωL-\frac{1}{ωC}}{R})$$