皆さんこんばんにちは、ユウです。
今回はC言語を用いた積分方法について紹介していきたいと思うよ!
今回の記事を読むメリット
✅プログラミングで積分が解けるようになる!
✅積分の基礎的な事が身につく!
✅プログラムは繰り返し処理を行っているだけだと分かる!
数値積分
今回は区間[a,b]で連続な関数y=f(x)の定積分を行っていきます。
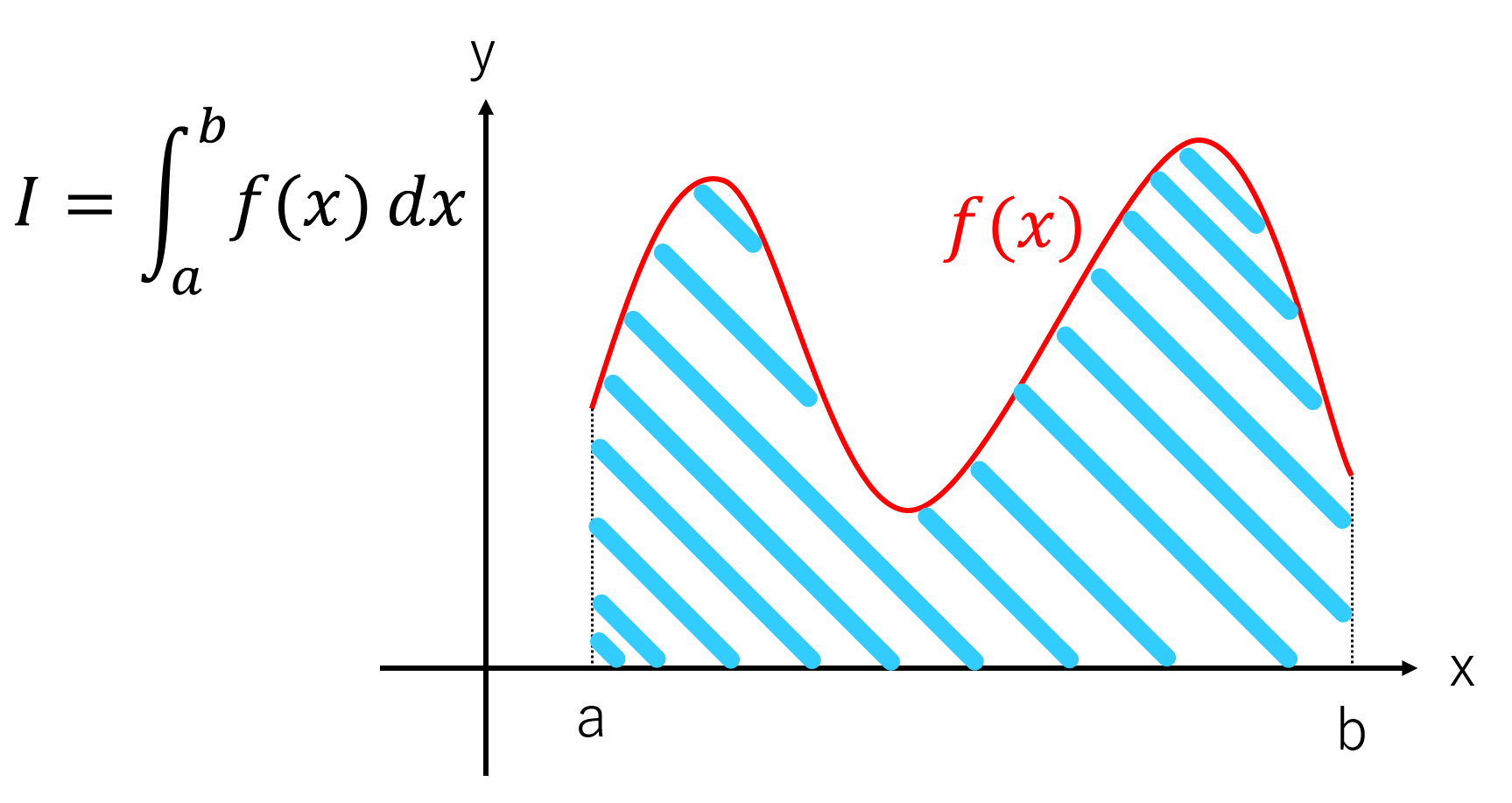
x=a,x=b,y=f(x)とx軸で囲まれた面積を求める際、簡単な計算だった場合は手計算でやった方が早いかもしれませんが、難しい関数の場合はかなりの労力が必要となりますよね。
そこで、計算機(コンピュータ)で数値的に近似値を求めることで積分値を導出します。
計算機による積分方法は区分求積法、ニュートン・コーツ求積法、ロンバーグ法等といった方法が存在します。
今回はその中の区分求積法と、ニュートン・コーツ求積法について紹介していきたいと思います。
区分求積法
・最も簡単な積分の導出方法
ニュートン・コーツ求積法
・台形公式
・シンプソンの公式を用いる
ロンバーグ法
・台形公式により逐次近似法
・計算速度が速く、すくな計算量で必要な計算精度が得られる
※ロンバーグ法については今後の記事で説明していきます。
区分求積法
定積分を細長い長方形の面積の和とする。
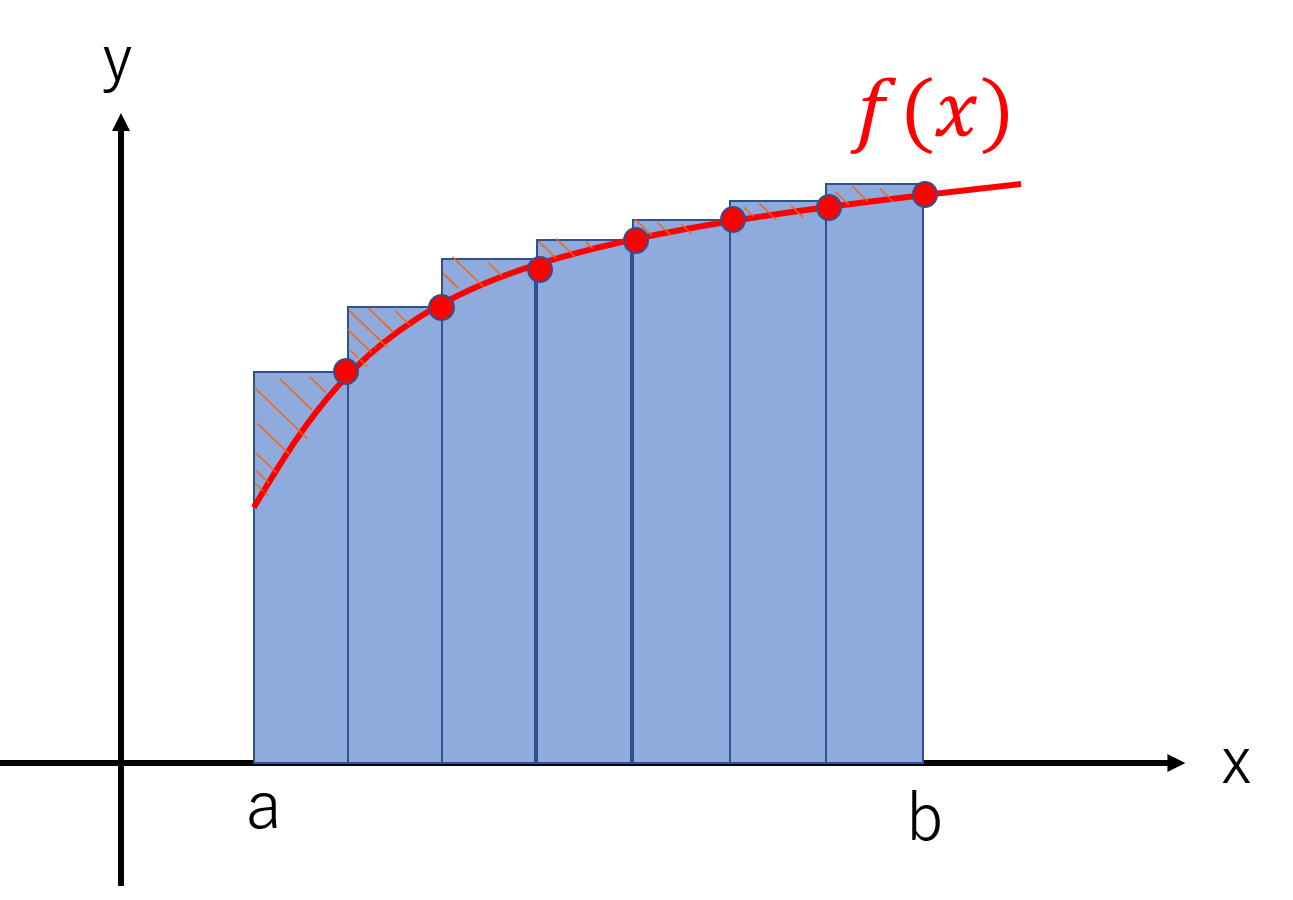
ある関数f(x)を四角形で区切っていくと上の図のようになります。
積分は、関数における区間の面積を求めると同じ意味です。
ですので、この四角形の面積を求めていくことで、積分での値を求めていきます。
しかし、上の図のように四角形の幅が広いと斜線部のように余計な部分が存在してしまします。
これではまともな値は導出されません。これを解決する方法は四角形の幅をかなり小さくすれば解決することが出来ます。
そうすることで、関数の値に小さいxの値を代入し、幅x1-xと高さf(x1)でかなり細い四角形を求めます。(x1はxの次にくる値)
そして、その四角形を指定した区間まで、足し合わせればその関数が表わす面積を求めることが出来ます。
区分求積法原理はこれだけです。
区分求積法の数式
\[\int_{a}^{b} f(x) \, dx \cong \sum_{j=1}^n f(x_{j-1})(x_{j}-x_{j-1}) = h \sum_{j=1}^n f(x_{j-1})\]
ニュートン・コーツ公式
分点を以下の様に取ります。\[a=x_{0}<x_{1}<x_{2}<\dots<x_{n}=b\]
\[f_{k}=f(x_{k})\]を通るラグランジュ補間多項式\[P_{n}(x)\]を考えます。
ただし、分点は等間隔\[h=\frac{b-a}{n}\]で並んでいるとしています。
このIを以下の様に近似します。
\[I_{n} = \int_{a}^{b} P_{n} (x) \, dx \]
この式内の
\[P_{n}(x)\]
は多項式なので手計算でも簡単に解くことが出来ます。
このように、ラグランジュ補間多項式を利用して数値積分を行う方法をニュートン・コーツの積分公式といいます。
\[P_{n}(x)= \sum_{k=0}^{n} f_{k} l_{k} (x) \]
と書くと以下の様に変形することが出来ます。
\[\int_{a}^{b} P_{n} (x) \, dx = \sum_{k=0}^{n} f_{k} \int_{a}^{b} l_{k} (x) \, dx = \sum_{k=0}^{n} a_{k} f_{k} \]
ただし、
\[a_{k} = \int_{a}^{b} l_{k} (x) \, dx \]
この近似積分公式を(n+1)点のニュートン・コーツ公式といいます。
ニュートン・コーツ求積法の数式
\[\int_{a}^{b} P_{n} (x) \, dx = \sum_{k=0}^{n} f_{k} \int_{a}^{b} l_{k} (x) \, dx = \sum_{k=0}^{n} a_{k} f_{k} \]
ただし、
\[a_{k} = \int_{a}^{b} l_{k} (x) \, dx \]
台形公式
上記で紹介したニュートン・コーツ公式を応用すると、台形公式が求まります。
\[\sum_{k=0}^{n-1} \frac{h}{2} (f_{k} + f_{k+1}) \]
ただし、
\[h = \frac{b-a}{n} \]
これは、小さな台形の面積を求め、それを足し合わせているだけです。
先ほどの区分求積法では、長方形の面積を足し合わせて積分値を求めていましたが、今回は台形で求めているので、より正確な値を導出することが出来ます。
因みに台形の公式は、(上底+下底)×高さ/2です。
台形公式のアルゴリズム
以下にアルゴリズムを示しておきます。
参考程度に見て下さい。
Input a,b,n
h ← (b-a)/n
T ← (f(a)+f(b))/2
For i=1,2,…,n-1
T ← T+f(a+ih)
end for
T ← hT
Output T
ソースコード
今回は以下の公式がどのくらいまで正確に解けるか確認するコードとなります。
\[\int_{1}^{2} \frac{2}{x^2} \, dx = 1\]
\[\int_{0}^{1} \frac{4}{1+x^2} \,dx = \pi \]
最後に
今回は、アルゴリズムを用いた積分方法について紹介していきましたが、案外小学生や中学生で習った公式で積分が簡単に解けると言うことが分かったかと思います。
この記事を通して気づいてもらえたかと思いますが、今回のアルゴリズムはいかにしてい関数と仮定した面積との空白をなくすかが、肝となります。
あなたの考え次第で、プログラムの処理速度の違いが出てくるかもしれないので、ぜひ自分で効率の良いプログラムを組んでみてはいかがでしょうか。
今回はこれで以上となります。
最後まで読んでいただきありがとうございます!


















