どうも,ユキです。
今日は,空間ベクトルの入試問題を解いていきましょう。
記事の内容
☑ベクトルの大学入試1次試験レベルの問題
☑ベクトルで三角錐の体積を求める
問題
正方形ABCDを底面とする正四角錐OABCDがあり,各辺の長さは1である。底面の対角線の交点をEとし,\(\overrightarrow{OF}=\frac{3}{2}\overrightarrow{OE}\)となる点Fをとる。また,辺OA上に点Pを,直線BF上に点QをPQ⊥OAとなるようにとる。以下,\(\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b},\overrightarrow{OC}=\overrightarrow{c}\)とおき,実数\(s\),\(t\)を用いて,\(\overrightarrow{OP}=s\overrightarrow{a},\overrightarrow{BQ}=t\overrightarrow{BF}\)と表せるとする。このとき,以下の問に答えなさい。
(1) \(\overrightarrow{a}・\overrightarrow{b},\overrightarrow{b}・\overrightarrow{c},\overrightarrow{c}・\overrightarrow{a}\)をそれぞれ求めなさい。
(2) \(\overrightarrow{OQ}\)を\(s,t,\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\)を用いて表しなさい。また,\(s\)と\(t)の関係式を求めなさい。
(3) 三角形CPQの重心をRとする。点Rが平面ABC上にあるとき,\(\overrightarrow{OR}\)を求めなさい。
(4) 三角形BDRの面積を求めなさい。更に,三角錐FBDRの体積を求めなさい。
解答
(1)解答
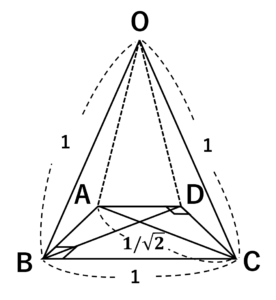
図1.各辺の長さが1の正四面体OABCD
\(\overrightarrow{a}・\overrightarrow{b}=\overrightarrow{b}・\overrightarrow{c}=1・1・\cos 60^°=\frac{1}{2}\)
\(\overrightarrow{a}・\overrightarrow{c}=|\overrightarrow{OA}|・|\overrightarrow{OB}|\cos 90^°=0\)
(2)解答
\(\overrightarrow{OQ}=\overrightarrow{OB}+\overrightarrow{BQ}\)
\(=\overrightarrow{OB}+t\overrightarrow{BF}\)
\(=\overrightarrow{OB}+t(\overrightarrow{OF}-\overrightarrow{OB})\)
\(=(1-t)\overrightarrow{OB}+\frac{3}{2}t\overrightarrow{OE}\)
\(=(1-t)\overrightarrow{OB}+\frac{3}{2}t(\frac{\overrightarrow{OA}+\overrightarrow{OC}}{2})\)
\(=(1-t)\overrightarrow{OB}+\frac{3}{4}t(\overrightarrow{OA}+\overrightarrow{OC})\)
<終>
また,\(s,t\)の関係式について,PQ⊥OAより,
\(\overrightarrow{PQ}・\overrightarrow{OA}=0\)
\((\overrightarrow{OQ}-\overrightarrow{OP})・\overrightarrow{OA}=0\)
\((\overrightarrow{OQ}-s\overrightarrow{OA})・\overrightarrow{OA}=0\)
\(\overrightarrow{OA}・\overrightarrow{OQ}=s\tag{1}\)
先ほど求めた\(\overrightarrow{OQ}\)に,\(\overrightarrow{OA}\)との内積をとると,
\(\overrightarrow{OA}・\overrightarrow{OQ}={(1-t)\overrightarrow{OB}+\frac{3}{4}t(\overrightarrow{OA}+\overrightarrow{OC})}・\overrightarrow{OA}\)
\(\overrightarrow{OA}・\overrightarrow{OQ}=\frac{3}{4}t+\frac{1}{2}(1-t)\)
\(\overrightarrow{OA}・\overrightarrow{OQ}=\frac{1}{4}t+\frac{1}{2}\tag{2}\)
式(1)=式(2)より,\(s\)と\(t\)の関係式は,
\(s=\frac{1}{4}t+\frac{1}{2}\tag{3}\)
<終>
(3)解答
Rは三角形CPQの重心なので,
\(\overrightarrow{OR}=\frac{\overrightarrow{OC}+\overrightarrow{OP}+\overrightarrow{OQ}}{3}\)
\(=\frac{\overrightarrow{OC}+s\overrightarrow{OA}+(1-t)\overrightarrow{OB}+\frac{3}{4}t(\overrightarrow{OA}+\overrightarrow{OC})}{3}\)
\(=(\frac{1}{3}+\frac{1}{4}t)\overrightarrow{OC}+\frac{1}{3}(1-t) \overrightarrow{OB}+(\frac{1}{3}s+\frac{1}{4}t)\overrightarrow{OA}\)
\(s+t+u=1\)より,
\(\frac{1}{3}+\frac{1}{4}t+\frac{1}{3}(1-t)+\frac{1}{3}s+\frac{1}{4}t=1\)
\(\frac{1}{6}t+\frac{1}{3}s+\frac{2}{3}=1\)
\(\frac{1}{3}s=-\frac{1}{6}+\frac{1}{3}\)
\(s=-\frac{1}{2}t+1\tag{4}\)
ここで,(2)の答えを利用します。
式(3)と式(4)を連立すると,
\(s=\frac{1}{4}t+\frac{1}{2}\)
\(s=-\frac{1}{2}t+1\)
\(s\),\(t\)はそれぞれ,
\(s=\frac{2}{3}\)
\(t=\frac{2}{3}\)
\(s,t\)を\(\overrightarrow{OR}\)に代入すると,
\(\overrightarrow{OR}=\frac{1}{3}((\frac{3}{4}\frac{2}{3}+\frac{2}{3})\overrightarrow{OC}+(1-\frac{2}{3})\overrightarrow{OB}+(\frac{3}{4}\frac{2}{3}+1)\overrightarrow{OC})\)
\(\overrightarrow{OR}=\frac{7}{18}\overrightarrow{OA}+\frac{1}{9}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}\)
(4)解答
三角形の比を使って解きます。
三角形BDRの面積は,三角形ABDの面積を用いて表すと,
\(\triangle BDR=\frac{R’R}{AR’}\triangle ABD\tag{5}\)
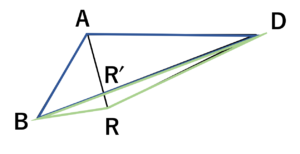
図2.三角形の面積比
まず,\(\frac{R’R}{AR’}\)を求める為に,ベクトル\(\overrightarrow{AR}\)について考えていきましょう。
\(\overrightarrow{OR}=\frac{7}{18}\overrightarrow{OA}+\frac{1}{9}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}\)
\(\overrightarrow{AR}=\frac{1}{9}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}\)
R’が辺BD上にあることを利用したいのでもう少し変形します。
\(\overrightarrow{AR}=\frac{1}{9}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}\)
\(\overrightarrow{AR}=\frac{11}{18}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}\)
3点A,R,R’は一直線上に存在するので,
\(\overrightarrow{AR’}=\frac{11}{18}k\overrightarrow{AB}+\frac{1}{2}k\overrightarrow{AD}\)
R’は辺BD上に存在するので,
\(\frac{11}{18}k+\frac{1}{2}k=1\)
\(k=\frac{9}{10}\)
\(\frac{RR’}{AR’}\)は,
\(\frac{RR’}{AR’}=\frac{AR-AR’}{AR’}=\frac{10-9}{9}=\frac{1}{9}\tag{7}\)
続いて,三角形\(\triangle ABD\)の面積は,
\(\triangle ABD=\frac{1}{2}\tag{8}\)
式(7),式(8)より三角形\(\triangle BDR\)の面積は,
\(\triangle BDR=\frac{1}{9}\times \frac{1}{2}=\frac{1}{18}\tag{9}\)
更に,三角錐FBDRの体積\(V\)は,\(\triangle BDR\)と\(FE\)は垂直に交わるので,
\(V=\frac{1}{3}\times \triangle \times |FE|\)
と表されます。
\(|FE|=\frac{1}{2}|OE|=\frac{\sqrt{6}}{4}\)
よって,体積\(V\)は,
\(V=\frac{1}{3}\times \frac{1}{18} \times \frac{\sqrt{6}}{4}\)
\(V=\frac{\sqrt{6}}{216}\)
<終>
まとめ
ベクトルの分解
$$\overrightarrow{OQ}=\overrightarrow{OB}+\overrightarrow{BQ}$$
変数が2つ出てきたら方程式を2つ立てる
点Rが3点A,B,Cの定める平面上にあるとき,
\(\overrightarrow{AR}=r\overrightarrow{AB}+(1-r) \overrightarrow{AC}\)
三角形の面積は面積比で解く。
三角錐の体積は,1/3×底面積×高さで求める
関連問題へのリンク
問題まとめページー>
https://cupuasu.club/tag/highschool-math/
最後に
三角錐の体積を求めるのは面倒ですよね。実は,作問者側も三角錐の体積を求めさせるのは面倒に感じます。なので,問題を解く人にはわからないように隠しゴール的なものを用意して作問する場合が多いです。マリオメーカーをやったことがある人なら作問者の気持ちがわかるのではないでしょうか。


















