席替えで好きな人と隣の席になりたいけれど,なかなかなれない。
これって神様のいたずら?
今日は,好きな人と隣の席になる確率を求めていこうと思います。
この記事を読むメリット
☑好きな人と隣になる確率がわかる
好きな子と隣になる確率:席替えとは?
席替えは学校生活の楽しみの1つとして良く行われます。
因みに私の学校では,くじ引きで席替えをやっていました。
くじ引きで席を決められる時のあのスリル感はたまりませんねぇ。
そして,好きな子と隣の席になったときのあの高揚感は今でも忘れられません。
あの頃に,戻りてぇ~な~。
ここで,「生徒側の席替えをするメリット」と「先生側の席替えをするメリット」について考えます。
1. 友達ともっと仲良くなれる
2. 授業への集中を促す
「生徒側のメリット」
席替えをすることで,クラスの友達と親睦を深めることができます。
私のように,席が近くのお友達としか話せない人にとって,友達と良い関係を築くこの上ないチャンスです。
「先生側のメリット」
席替えをした後の授業は,席替えをする前の授業と比べて,授業中の私語が少なくなるものです。
先生方は,生徒たちに授業に集中して欲しいという思いで,席替えをしているのですね。
席替えで好きな子と隣になる確率
やった~。3回連続で好きな子と隣の席になれた~!
あ~。今年は,好きな子と1回も席が近づかない。
そして,席替えの度にこういう愚痴を友達とこぼしあっていたのは良い思い出です。
40人クラスのとき
それでは,40人クラスで,好きな子と席が隣になる確率(\(=P_{40}\))を計算しましょう。
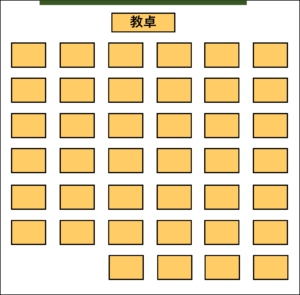
図1.40人クラスの机の配置
私の学校では,机の配置は,縦が6列でしたので,そちらを採用していこうと思います。
計算する確率\(P\)は,
\(P=\frac{自分と好きな子が隣になる場合の数}{自分と好きな子が席に座る全ての場合の数}\)
と計算すると求められます。自分と好きな子が隣になる場合の数を図にしてみました。

図2.好きな子と隣になる場合の数
\(P_{40}\)を計算すると,
\(P_{40}=\frac{40-7}{{}_40 \mathrm{C}_2}=\frac{33}{\frac{40・39}{2}}\)
\(P_{40}=\frac{11}{260}\) (4.2%)
となります。
ここで,\(C\)は高校数学に出てくる組み合わせというやつを使いました。
\(n\)人クラスのとき
いやいや,私のクラスは30人クラスで,縦8列です。
なんておっしゃる方がいらっしゃるかもしれないので,クラスの人数と列数に任意性を持たせてみました。
\(n\)人クラスのとき,好きな子と席が隣になる確率を\(P_n\)として,計算しましょう。
まず,\(n\)人クラスの机の配置です。
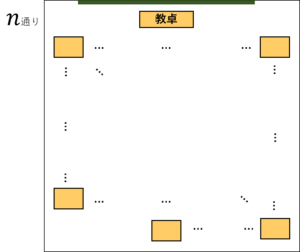
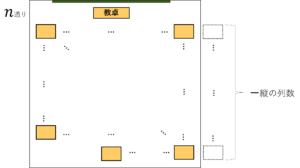
図3.\(n\)人クラスの席配置
このとき,縦に1列分だけ席を追加したら,好きな子と席が隣になる場合の数は\(n\)通りになります。
図4.好きな子と席が隣になる場合の数
したがって,\(n\)人クラスのとき,好きな子と席が隣になる確率\(P_n\)は,
\(P_n=2\frac{n-横の列数}{n(n-1)}\tag{1}\)
となります。
40人クラスで,縦の列数が\(k\)列のときの,好きな子と席が隣になる確率\(P\)は,
\(P=2\frac{40-7}{40・39}=\frac{11}{260}\)
となり,確かに先ほどの答えと一致します。
10回中少なくとも1回は好きな子と隣の席になる確率
1回で好きな子と席が隣になる確率を\(P\),とすると,10回中少なくとも1回は好きな子と隣になる確率\(S_10\)は,
\(S_{10}=1-\underbrace{(1-P)^{10}}_{1回も好きな子と隣にならない確率}\)
となります。
例えば,\(P=\frac{11}{260}\)を代入すると,\(S_{10}\)
\(S_{10}=1-(\frac{249}{260})^{10} \) (35%)
40人クラスだと,35%の確率で好きな子と隣になれます!
あまり高い数字ではありませんね。
もし,好きな子と席が隣になったら,神に感謝しましょう。
好きな子が前後左右に来る場合の確率
更に追求して,好きな子が前後左右に来る確率を求めてみましょう。
\(n\)人クラスのときの好きな子と席が近くなる確率
\(n\)人クラスの席配置を考えましょう。
先ほどと同様にして好きな子の席が自分の席の前後左右である確率を求めましょう。
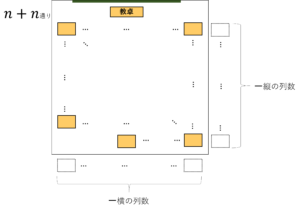
図5.好きな子の席が自分の席の前後左右である場合の数
縦一列と横一列に席を追加したとき,好きな子の席が自分の前後左右となる場合の数は,\(2n\)通りになります。
\(n\)人クラスのとき,好きな子の席が自分の前後左右となる確率\(P_n\)は,
\(P_n=\underbrace{2\frac{n-横の列数}{n(n-1)}}_{好きな子が左右に来る確率}+\underbrace{2\frac{n-縦の列数}{n(n-1)}}_{好きな子が前後に来る確率}\)
となるので,式を整理すると,
\(P_n=2\frac{2n-横の列数-縦の列数}{n(n-1)}\tag{2}\)
となります。
40人クラスで,縦の列数が6列,横の列数が7列の机配置の場合の確率\(P_n\)は,
\(P_n=2\frac{2・40-7-6}{40・39}=\frac{73}{780} \) (9.4%)
となります。
10回に1回くらいは,好きな子とお近づきのチャンスを得られるということですね。
10回中少なくとも1回は好きな子と席が近くなる確率
確率\(S_{10}\)は,好きな子の席が前後左右に来る確率\(P\)を用いて表すと,
\(S_{10}=1-(1-P)^{10}\)
\(P=\frac{73}{780}\)を代入すると,
\(S_{10}=1-(\frac{707}{780})^2\) (62.6%)
つまり,40人クラス,縦6列,横7列の机配置のとき,10回くらい席替えが行われれば,6割くらいの確率で好きな子の席が自分の席の前後左右に来ます。
好きな子と隣になる確率:まとめ
クラスの人数が\(n\)人のとき,好きな子と隣になる確率\(P_n\)は,
$$P_n=2\frac{n-横の列数}{n(n-1)} $$
クラスの人数が\(n\)人のとき,好きな子の席が自分の席の前後左右になる確率\(P_n\)
$$P_n=2\frac{2n-横の列数-縦の列数}{n(n-1)}$$
最後に
話は変わりますが,私は「からかい上手の高木さん」という漫画が好きです。
その主人公である「西片」とヒロインの「高木さん」が入学式で席が隣同士になるのですが,その確率を計算してみたいですね。