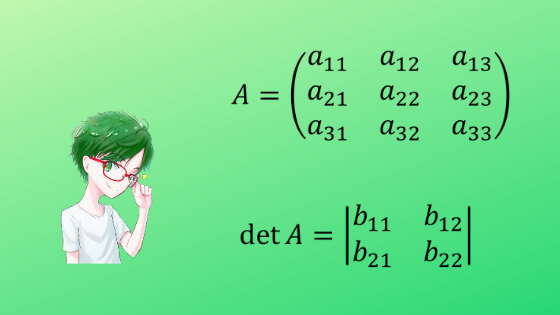独学で勉強しているけれど,どうしてもわからない所があるんだよなぁ。
どうも,ユキです。
今日は,過去の自分に向けた記事で,線形代数学をどのように勉強したらいいのかを懇切丁寧に解説します。
この記事を読むメリット
☑線形代数学の攻略法がわかる
線形代数学とは?
あれ,大学に入ってからベクトルの基礎を学ぶの?
線形代数学は,大学数学の基礎科目ですが,
線形代数学のような基礎科目で頑張った人が,後の専門科目でも好成績を収めています。
ただし,線形代数学は突き詰めると結構難しい学問です。
もちろん,単位を取ること自体は簡単な科目ですが,(大学1年生の前期に履修する。)
大学3年生の私(線形代数学80/100点以上とった)でも,未だに線形代数学の参考書でわからない所があります。
ということで,弊記事では,線形代数学で重要な所や難しい概念を解説し,なるべく皆さんに無駄を省いた勉強法を教えます。
線形代数学の目次:

線形代数学で重要な箇所のみピックアップします。
ここで,私が上げる重要な箇所は,大学の定期試験に出題されたり,他の科目の単位を取るのに役に立ったものをピックアップしています。
それがこちら、
1. 行列(行列の四則演算)
2. 逆行列,対称行列,交代行列,直交行列,ユニタリー行列
3. 連立1次方程式の解法(掃き出し法)
4. クラメールの公式
5. 行列式の性質
6. ラプラスの余因子展開,サラス展開
7. 部分空間
8. 固有値,固有ベクトル
9. 対角化
10. グラムシュミット直交化法
これらが一応,大学の授業で勉強した内容になっています。その中で,大事そうな箇所に焦点を当てて解説します。
連立1次方程式の解法(掃き出し法)
掃き出し法を使うと,連立1次方程式が解けるようになります。
ここは線形代数学の本を見れば理解できます。
私の場合は,掃き出し法の操作を参考書の例題を書き写すことで理解しました。
連立1次方程式を解けるようになったら,次は,クラメールの公式を勉強してください。
クラメールの公式はめちゃくちゃ便利です!
クラメールの公式は,連立1次方程式を解く方法の1つとして知られているものです。
ちなみに私は,クラメールの公式のおかげで,「電気回路学」,「電磁気学」,「制御工学」,「自動制御」などの単位を取ることができました。
行列式,サラス展開,ラプラスの余因子展開
線形代数学初心者の人は特に勘違いしやすいのですが,行列と行列式は全く違います。
ひとえに違いを述べるとしたら,行列はベクトル(大きさ+向き)で,行列式はスカラー(大きさ)です。
↓行列↓
\(A=\left(
\begin{array}{ccc}
a_{11}& a_{12}& a_{13}\\
a_{21}& a_{22}& a_{23}\\
a_{31}& a_{32}& a_{33}
\end{array}
\right)\)
↓行列式↓
\(\det A=\left|
\begin{array}{ccc}
a_{11}& a_{12}& a_{13}\\
a_{21}& a_{22}& a_{23}\\
a_{31}& a_{32}& a_{33}
\end{array}
\right|\)
行列式の例:\(\left |\begin{array}{ccc}
1& 2\\
3& 4\\
\end{array}
\right|
=1・4-2・3=-1\)
そんな行列式ですが,3×3の行列式の計算ができるようになったら,
行列式の8つの性質を参考書の問題の計算を使って理解してください。
これは,大学の授業を受ければ一瞬でできると思いますが,自分の手で実際に計算をして理解しましょう。
サラス展開とラプラス余因子展開の勉強法は,
サラス展開は,3×3の行列式を計算する為の公式で,
ラプラス余因子展開は,3×3以上の行列式を計算する為の公式です。
私の場合,サラス展開を先に丸暗記して,ラプラス余因子展開を覚えましたが,
ラプラス余因子展開から先に覚えればよかったと後悔しています。
サラス展開は,ラプラス余因子展開から生まれた副産物なので,ラプラス余因子展開から導出ができます!
固有値,固有ベクトル,対角化
固有値と固有ベクトルは,対角化を行う為に必須の知識です。
また,固有値と固有ベクトルは,統計学や量子力学に応用されています。
統計学では因子分析。量子力学では固有エネルギーを求める問題を解くときに使います。
固有値と固有ベクトルは,定期テストにも出題しやすい箇所なので勉強は必須です。
私の場合固有値と固有ベクトルも,参考書の例題で計算自体は理解できましたが,固有値や固有ベクトルの概念は,授業を聞かないとなかなか理解出来ませんでした。
固有値,固有ベクトルを計算出来るようになると,対角化をできるようになるので,ベクトル\(A\)の\(n\)乗(\(A^n\))の計算を簡単に行うことができます。
グラムシュミット直交化法
グラムシュミット直交化法は,1つ1つのベクトルを直交化して,\(xyz\)直交座標系のような軸を無数に作り出すことができます。
グラムシュミット直交化法の難しい所は,式が複雑な所ですね。
頭が良い人はすんなり理解出来るのでしょうが,私は講義で説明を聞いてようやく理解しました。
グラムシュミット直交化法:
\(x_1,x_2,\cdots,x_n\)の一次独立な\(n\)個のベクトルから\(a_1,a_2,\cdots,a_n\)の基底ベクトルを作る方法です。
\(y_1=x_1,a_1=\frac{y_1}{|y_1|}\)
\(y_2=x_2-(x_2・a_1)a_1,a_2=\frac{y_2}{|y_2|}\)
\(y_n=x_n-\sum_{k=1}^{n-1} (x_n・a_k)a_k,a_n=\frac{y_n}{|y_n|}\)
なお,グラムシュミット直交化法は難しいので、テストにも出題されやすいですが,今後の専門科目には一切役に立ちません。
線形代数学の勉強法

結論,線形代数学は,自分で手を動かして計算をすれば,自然に身につきます。
私がやっていた線形代数学の勉強法
一例として私がいつもやっている公式の覚える3ステップを解説します。
1. 公式は教科書を見ながらでいいから自分の手で導出する
2. 1.で覚えられない公式は,図を書いてイメージで覚える
3. 例題の答えを書き写して解答の流れを押さえる
公式の導出をすると,もし仮に記憶が曖昧になっても思い出すことができます。
いちいち導出するのも面倒くさいと思われる方もいらっしゃるかと思いますが,
その面倒くさいという気持ちがプラスに作用して,脳に公式を叩き込む事ができるわけです。
しかし,導出が難しい公式があるのも事実。そんなときは,イメージで覚えましょう。
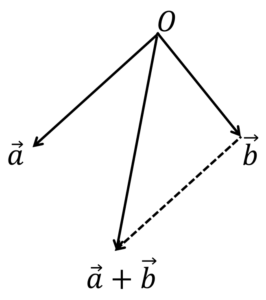
例えば,シュワルツの不等式は,
$$|\overrightarrow{a}+\overrightarrow{b}| \leq |\overrightarrow{a}|+|\overrightarrow{b}|$$
\(\overrightarrow{a},\overrightarrow{b}\)をそれぞれ三角形の辺の長さに対応させると簡単に覚えられます。

Youtubeなどを活用して勉強するといい
Youtubeで「線形代数学」と検索すれば,線形代数学の勉強はできます。
私は,「筑波大学」や「慶應大学」といった大学が出している動画を視聴し,ノートをとりながら勉強していました。
最後に
医学部で線形代数学は使わないと聞いて驚きました。
確かに患者さんの手術で線形代数学を使っている所を想像できません。
理学部,工学部は線形代数学を勉強するのですが,大学3年生の時分は,あまり使ってないですね。