[面白い数学] フィボナッチ数列について（勉強するのはあなたの番です）

ウサギが一匹，ウサギが二匹，ウサギが三匹，ウサギが五匹，ウサギが八匹，ウサギが一三匹。どうも，ユキです。

今回は，死なないウサギの無限増殖を数列に落とし込んだフィボナッチ数列についてのお話をします。

ドラマ「あなたの番です」に出てきたみたいですね。（あまり知らなくてすいません）

フィボナッチ数列を学ぶメリット

1．フィボナッチ数列から，大学入試に出てくる隣接3項間の漸化式の解法を学べます

2．極限の問題の発想を理解できます。

3．数学のチート技である解析接続に触れることが可能です

フィボナッチ数列とは

問題：ある1組のウサギの夫婦がいるとします。ウサギの夫婦は，毎日1組のウサギを生みます。そして，生まれたウサギの組は，生まれてから1日で成長し，1組のウサギの夫婦になります。1組のウサギが生まれたときを1日目とすると，$n$日後には，ウサギの組は何組になりますか？ただし，ウサギは，永久に死なないものとします

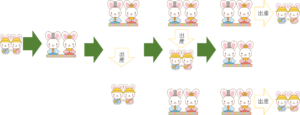
図1．ウサギが増える様子

図からウサギは次のように増えていきます。

図から1日目，2日目はウサギが1組で，3日目はウサギが2組，4日目はウサギが3組，5日目は，$\cdots$

眠くなってきますね(^▽^)。では，数列で書きましょう。

1，1，2，3，5，8，13，21，34，55，89，144，233，$\cdots$

この数列を見ると，なにか気づくことはありませんか？

実は，この数列は，連続した2項を足すと，次の項の数になります。
1＋1＝2，1＋2＝3，2＋3＝5，3＋5＝8，5＋8＝13，8＋13=21，13+21=34，21+34=55，55+89=144，89+144=233，$\cdots$

なぜ，連続した項を足すと次の項の数が求まるのでしょうか？

<証>
$n$日目のウサギの組数を$a_{n}$とします。ここで，$a_{n+1}$組のウサギの中で，生まれたばかりのウサギの組数$\alpha$は，
$\alpha=a_{n+1}-a_{n}\tag{1}$
となります。

また，$\alpha$は，$n-1$日目のウサギの組数$\alpha$に相当する(図2参照)ので，

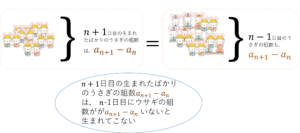
図2．$\alpha$は，$n-1$日目のウサギの組数

$\alpha=a_{n-1}$

が成立し，式(1)の$\alpha$に代入すると，

$a_{n-1}=a_{n+1}-a_{n}$
が成立します。よって，
$$a_{n-1}+a_{n}=a_{n+1}\tag{2}$$
が成立し，連続した項を足すと次の項の数が求まることが示せました。

式(2)のような数列の式を漸化式といい，一般的にフィボナッチ数列の漸化式は，
$$a_{n+2}=a_{n+1}+a_{n}$$
$a_1=a_2=1$
で表されます。

これは，漸化式の中でも，隣接3項間漸化式と呼ばれていて，大学入試でも出題されています。

フィボナッチ数列いろいろ

フィボナッチ数列の一般項
$$a_{n}=\frac{1}{\sqrt{5}}(\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n $$
一般項の求め方は，別の記事で取り上げます。

フィボナッチ数列と黄金比
$$\displaystyle \lim_{n \to \infty} \frac{a_{n+1}}{a_{n}}=\frac{\sqrt1+{5}}{2}$$
$\frac{1+\sqrt{5}}{2}$は黄金比とも呼ばれています。
この極限の求め方は，別の記事で解説します。

フィボナッチ数列の無限和が-1？
$$1+1+2+3+5+\cdots=-1$$

え，嘘だろ？正の数を無限個足すと数はマイナス？

この記事も別の記事で解説します。