自動制御の基本問題になっているので,最低でも,この問題を解けるようになってください。
この記事を読むメリット
☑自動制御の基本問題を解くことが出来るようになる。
自動制御演習問題2019
問題1:
問題1:
下記の(1),(2)それぞれの伝達関数について,入力\(u(t)\)の単位ステップ入力に対する出力の時間応答\(y(t)\)を求めよ。
\(Y(s)=G(s)U(s)\)
(1) \(G(s)=\frac{1}{s+3}\)(2) \(G(s)=\frac{6}{s^2+4s+3}\)
問題1解答:
\(u(t)\)は単位ステップ入力なので,\(U(s)\)は次のように表される。
\(U(s)=\frac{1}{s}\)
(1) 解答
\(Y(s)=\underbrace{\frac{1}{s+3}}_{G(s)}\underbrace{\frac{1}{s}}_{U(s)}\)
ここで,ヘヴィサイドの展開定理を用いて,部分分数分解を行うと,
\(Y(s)=\frac{1}{3}(\frac{1}{s}-\frac{1}{s+3})u(t)\)
\(Y(s)\)を逆ラプラス変換すると,
\(y(t)=\frac{1}{3}(1-e^{-3t})u(t)\)
(2) 解答
\(Y(s)=\underbrace{\frac{6}{s^2+4s+3}}_{G(s)}\underbrace{\frac{1}{s}}_{U(s)}\)
ここで,ヘヴィサイドの展開定理を用いて,部分分数展開を行うと,
\(Y(s)=2\frac{1}{s}-3\frac{1}{s+1}+\frac{1}{s+3}\)
\(Y(s)\)を逆ラプラス変換すると,
\(y(t)=(2-3e^{-t}+e^{-3t})u(t)\)
<終>
問題2:
問題2:
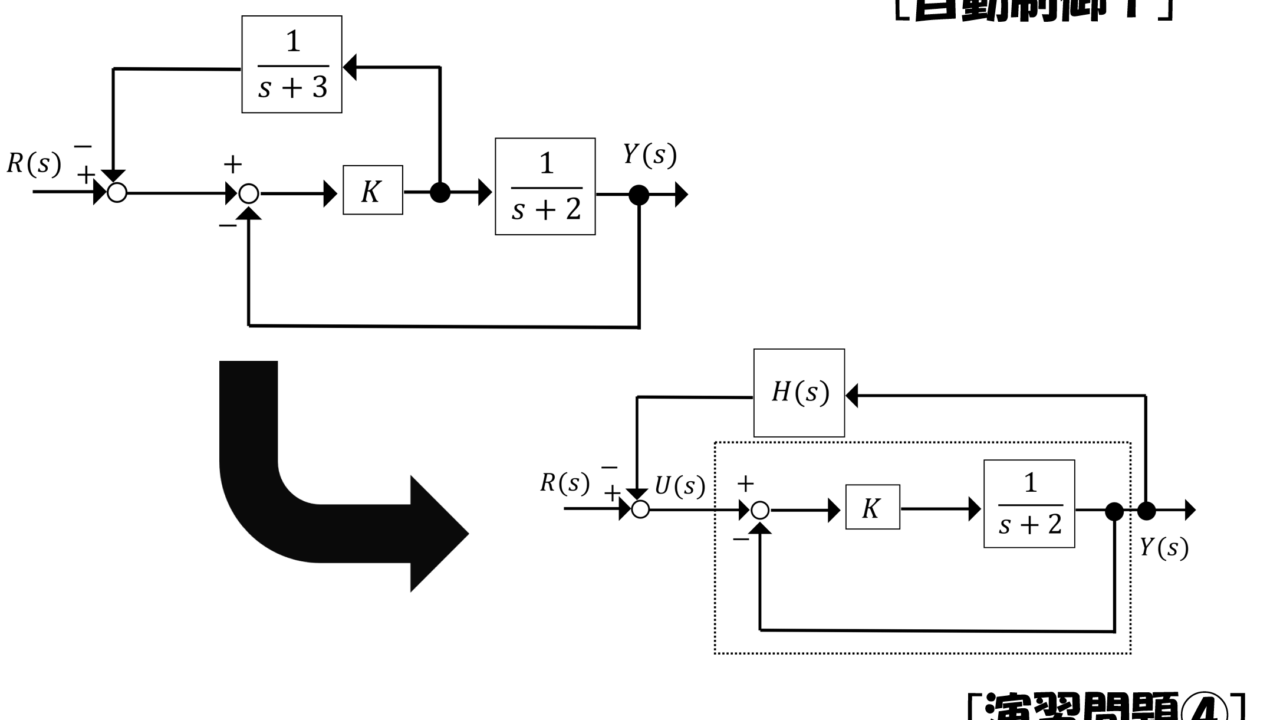
下記のブロック線図で(a)⇒(b)の等価変換を行い,システム全体の伝達関数を求めたい。このとき,各問に答えよ

(a)

(1) (b)の伝達関数\(H(s)\)を求めよ。
(2) (b)の点線枠内の伝達関数\(G_1(s)=\frac{Y(s)}{U(s)}\)を求めよ。
(3) システム全体の伝達関数\(G_{c1}(s)=\frac{Y(s)}{R(s)} \)を求めよ。
問題2解答:
(1) 解答
\(H(s)=\frac{1}{s+3}(\frac{1}{s+2})^{-1}=\frac{s+2}{s+3}\)
(2) 解答
\(G_1(s)=\frac{K\frac{1}{s+2}}{1+K\frac{1}{s+2}}=\frac{K}{s+2+K}\)
(3) 解答
\(G_{c1}(s)=\frac{\frac{K}{s+2+K}}{1+\frac{s+2}{s+3}\frac{K}{s+2+K}}\)
\(G_{c1}(s)=\frac{K}{s+2+K+\frac{s+2}{s+3}K}\)
\(G_{c1}(s)=\frac{K(s+3)}{(s+2+K)(s+3)+(s+2)K}\)
\(G_{c1}(s)=\frac{K(s+3)}{s^2+(6+K)s+6+5K}\)
<終>
問題3:
問題3:
下記の伝達関数\(G(j\omega)\)の折れ線近似のボード線図(ゲイン特性,位相特性)を描け。
※横軸の範囲
対数軸で0.1~10000。縦軸の範囲:ゲイン特性は-40dB~40dBで20dB刻み,位相特性は-90°~90°で45°刻みとすること。また,最終的な合成波形がわかるように描くこと。
$$G(j\omega)=\frac{1+j\omega}{(1+0.1j\omega)(1+0.01j\omega)}$$
問題3解答:
\(G(j\omega)\)を3つの関数に分解する
\(G(j\omega)=\underbrace{(1+j\omega)}_{G_1(j\omega)}\underbrace{\frac{1}{0.1j\omega}}_{G_2(j\omega)}\underbrace{\frac{1}{1+0.01j\omega}}_{G_3(j\omega)}\)
すると,ボード線図は次のように描ける。
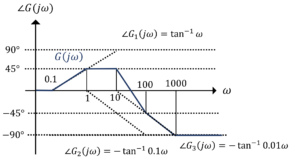
図1.ボード線図ー位相特性

図2.ボード戦図ーゲイン特性
問題4:
問題4:
下記のブロック線図について,各問に答えよ。
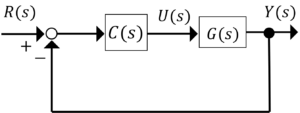
\(C(s)=K,G(s)=\frac{3}{s(s+2)(s+4)}\)
(1) 特性方程式を求めよ。
(2) ラウスの安定判別法により,安定な\(K\)の範囲を求めよ。
問題4解答:
(1) 解答
特定方程式は,
\(1+C(s)G(s)=0
\(s^3+6s^2+8s+3K\)
(2) 解答
(1)で得られた特性方程式に,ラウスの安定判別法を適用すると,
| \(s^3\) | 1 | 8 | 0 |
| \(s^2\) | 6 | 3K | 0 |
| \(s^1\) | -\frac{1・3K-8・6}{6} | 0 | 0 |
| \(s^0\) | -(-3K) | 0 | 0 |
ラウス表
ラウスの安定判別法より,
\(-\frac{1・3K-8・6}{6}<0\),\(3K>0\)
が導かれる。以上の2つの不等式を解くと,求める\(K\)の範囲は,
\(0<K<16\)
問題5:
問題5:下記の説明分の(ア)~(オ)に当てはまる適切な語句を答えよ。
A.1次形(1次遅れ系)の伝達関数によるステップ応答の速さは,(ア)によって決まり,(ア)が大きいほど応答が(イ)。
B.制御システムの特性方程式から得られる\(s\)の根を(ウ)とよぶ。全ての(ウ)の(エ)が負であるとき,制御システムは安定である。
C.伝達関数\(G(s)\)のインパルス応答\(g(t)\)と入力\(u(t)\)(ラプラス変換\(U(s)\))との(オ)をラプラス変換すると\(G(s)U(s)\)となる。
問題5解答:
(ア)時定数
(イ)遅い
(ウ)極
(エ)実数部分
(オ)畳み込み積分
まとめ
最後に
自動制御の基礎を学ぶことで,電験1種,電験2種の難関資格の合格に大きく近づけるでしょう。