$$\require{\cancel}$$
どうも,ユキです。
ギャンブルで勝てる人の割合を計算していたら,予想外の事実に気づいてしまいました。
この記事を読んで得られる知見
☑ギャンブルのプレイヤーはボロ勝ちする人orボロ負けする人しかない
☑パチンカスをぶっ壊す!
逆正弦法則:ギャンブルが強い人はごく一部

皆さんはパチンコ,競馬,スロット,麻雀,バイナリーオプションなどの投機をしますか?(私はしていません。)
今から,パチンコ,競馬,スロット,バイナリーオプションを稼ぐためのツールとして活用しようとしている人(またはすでにしている人)に,残酷な事実からお伝えしようと思います。
結論から言うと,ギャンブルをする人の大多数は大損します(´・д・`)
これは残念ながら,周知の事実です。
ギャンブルは,胴元が儲かる(お店が儲かる)ので,プレイヤーは,平均的に損をします。
ちなみに,日本で解禁されている公営ギャンブルは,胴元は25%程儲かっていると言われています。つまり,パチンコ,競馬,スロットは,還元率75%のギャンブルであると言えます。
バイナリーオプションはこれらのギャンブルとは異なり,金融商品(株,債券,外貨)の一種なので,還元率は80~100%くらいです。
ギャンブルをする人の大多数が大損している事実は,数学的に証明することができます。
その事実こそ,今回の記事のテーマである「逆正弦法則」です。
逆正弦法則とは?
確率は皆さんの直感を裏切ります。
逆正弦法則は,私達の直感を裏切る確率の一種です。
逆正弦法則とは,ギャンブルの勝率の分布関数\(F(x)\)が逆正弦分布をとっているという法則です。
逆正弦(通称:arcsin)とは,正弦(sin)の逆関数である(arcsin:「アークサイン」)を表します。
今,個々のゲームで勝つ確率を\(\frac{1}{2}\)とし,勝ち越し期間率を\(x\)とすると,(勝ち越し期間率は後ほど定義します。)
分布関数\(F(x)\)は,
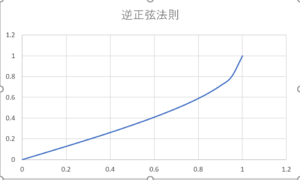
\(F(x)=\frac{2}{\pi} \arcsin (x)\)
図1.横軸:\(勝ち越し率=\frac{勝ち越し期間}{期間}\)
縦軸:勝ち越し率が\(x\)未満の人の割合
で表されます。
このグラフから,勝ち越し期間率が50%未満の人の割合は\(\frac{1}{2}\)であることが読み取れます。
しかし,私達は,勝ち越し期間率\(x\)の人がどのくらいの密度で存在するのかを知りたいので,分布関数\(F(x)\)を微分した密度関数\(f(x)\)を見ます。
密度関数\(f(x)\)は,
$$f(x)=\frac{1}{\pi}\frac{1}{\sqrt{x}\sqrt{1-x}}dx$$
グラフを描くと,
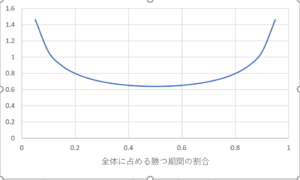
図2.横軸:\(勝ち越し率=\frac{勝ち越し期間}{期間}\)
縦軸:勝ち越し率が\(x\)の人の割合
このグラフによれば,勝ち越し率\(x\)を持つ人の割合は一定ではなく,負け組と勝ち組に二極化していることがわかります。
★逆正弦法則の特徴★
・勝率50%未満の人の割合は\(\frac{1}{2}\)
・極端に勝率が高い人と極端に勝率が低い人の割合が大きい
・勝率\(\frac{1}{2}\)の近傍の人の割合は低い
逆正弦法則:証明

逆正弦法則の密度関数\(f(x)\)は,
\(f(x)= \frac{1}{\pi}\frac{1}{\sqrt{x}\sqrt{1-x}}dx \)
で表されるという話をしましたが,
本当に逆正弦法則は成り立っているのでしょうか?
証明してみましょう。
ここで,勝率\(\frac{1}{2}\)のギャンブルは,対称なランダムウォークの運動に置き換えることができます。
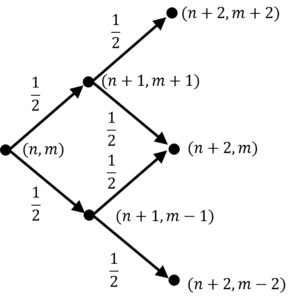
対称なランダムウォークの運動:
\(t-y\)座標系について,横軸\(t\)を時間,縦軸\(y\)を位置とする。時刻\(t=n\)に粒子が位置\(y=m\)にいれば,時刻\(t=n+1\)には粒子は,\(t=m+1\)または\(t=m-1\)のどちらかに移る。また,時刻が1進んだときに位置が+1に進む確率を\(\frac{1}{2}\)とする。
\(n,m\)は整数
粒子が,\(2n\)時間のうち\(2m\)時間を正の領域に,\(2n-2m\)時間を負の領域に滞在している事象を\(p_{2m,2n}\)とすると,
\(p_{2m,2n}=u_{2m}u_{2n-2m}={}_{2m} \mathrm{C}_{m}2^{-2m}・{}_{2n-2m} \mathrm{C}_{n-m}\)
となることが証明されています。
勝ち越し期間率\(x\)を\(x=\frac{m}{n}\)とすると,\(p_{2m,2n}\)は,
\(p_{2m,2n}≒f(x)=\frac{1}{\pi}\frac{1}{\sqrt{x}\sqrt{1-x}}\)
関数\(f(x)\)で近似されることを証明したい!
<証明>
\(p_{2m,2n}={}_{2m} \mathrm{C}_{m}2^{-2m}・{}_{2n-2m} \mathrm{C}_{n-m}\)
\( p_{2m,2n}=\frac{(2n)!}{n! n!}・\frac{(2n-2m)!}{(n-m)!(n-m)!}2^{-2n}\)
\(n ≫1,m≫1\)のとき,スターリングの公式\((n!≒\sqrt{2\pi n}n^n e^{-n})\)より,
\( p_{2m,2n}≒\frac{\sqrt{\cancel{2}\cancel{\pi} \cancel{2}\cancel{n}}(2m)^{2m} \cancel{e^{-2m}}}{\sqrt{\cancel{2} \cancel{\pi} m}m^m \cancel{e^{-m}}・\sqrt{\cancel{2}\pi m}m^m \cancel{e^{-m}}}・\frac{\sqrt{\cancel{2}\cancel{\pi} \cancel{2}\cancel{(n-m)}}(2n-2m)^{2n-2m} \cancel{e^{-(2n-2m)}}}{ \sqrt{\cancel{2}\cancel{\pi} \cancel{(n-m)}}(n-m)^{(n-m)} \cancel{e^{-(n-m)}}・\sqrt{\cancel{2}\pi \cancel{(n-m)}}(n-m)^{(n-m)} \cancel{e^{-(n-m)}}}2^{-2n}\)
\(=\frac{\cancel{2^{2m}}\cancel{m^{2m}}}{\sqrt{\pi}\sqrt{m} \cancel{m^{m}}・\cancel{m^{m}}}・\frac{\cancel{2^{2n-2m}} \cancel{(n-m)^{2n-2m}}}{\sqrt{\pi} \sqrt{n-m} \cancel{(n-m)^{n-m}}・\cancel{(n-m)^{n-m}}}\cancel{2^{-2n}}\)
\(=\frac{1}{\pi \sqrt{m}\sqrt{n-m}}\)
ここで,\(\frac{m}{n}=x\)とすると,
\(=\frac{1}{\pi}\frac{1}{\frac{m}{n}\sqrt{1-\frac{m}{n}}}\)
\(=\frac{1}{\pi}\frac{1}{\sqrt{x}\sqrt{1-x}}\)
よって,
\( p_{2m,2n}≒\frac{1}{\pi}\frac{1}{\sqrt{x}\sqrt{1-x}}=f(x)\)
であることを示せました。
逆正弦法則:分布関数\(F(x)\)の導出
分布関数\(F(x)\)は,密度関数\(f(x)\)を定積分したものなので,
\(F(x)=\int_{0}^{x}\frac{1}{\pi}\frac{1}{\sqrt{x}\sqrt{1-x}} dx\)
ここで,\(t^2=x\)とおくと,\(2t dt=dx\),\(t=\sqrt{x}\)が成立する。
また,積分範囲は\(0 \to t^2\)なので,
\(F(x)= \int_{0}^{t^2}\frac{1}{\pi}\frac{1}{\cancel{t} \sqrt{1-t^2}} 2\cancel{t} dt \)
逆正弦関数の積分公式\(\int \frac{1}{\sqrt{1-x^2}}dx =\arcsin x \)を利用すると,
\(F(x)=\frac{2}{\pi}[\arcsin t]_{0}^{t^2}=\frac{2}{\pi} \arcsin t^2\)
よって,\(F(x)\)は,
\(F(x)=\frac{2}{\pi}\arcsin x\)
また,\(F(1)\)=1となるので,分布関数の性質を満たしています。
逆正弦法則:非対称

非対称の場合,つまり,個々のゲームでの勝つ確率が\(p\)で負ける確率が\(1-p\)のゲームでは,アークサイン(逆正弦)の形になりません。
非対称の場合の\( p_{2m,2n}\)は,
\( p_{2m,2n}=u_{2m}u_{2n-2m}p^n(1-p)^n\)
で表されます。
そして,\( p_{2m,2n}\)の近似式\(f(x)\)は,\(x=\frac{m}{n}\)とすると,
\(f(x)=\frac{1}{\pi \sqrt{x}\sqrt{1-x}}[p(1-p)]^{mx}\)
となり,望まない\(m\)が残ってしまいます。
逆正弦法則:まとめ
・ギャンブルで勝ち越し期間率が高い人と低い人に二極化する
・非対称の場合は,分布関数がアークサインの形にならない
最後に
パチンコ・スロット,競馬などの公営ギャンブルをする人へ,
ゲームセンターのような感覚で遊びに行くのは大いに結構ですが,
公営ギャンブルはお金の増やすのに不向きな施設です。
お金を増やすのであれば,ブログ,資産運用などを始めればいいと思います。