センター試験のベクトルの問題が解けずに困っている。
どうも,ユキです。
数学のセンター試験は,わかる大問は満点とれたりするんですけれど,
わからないものはとことんわからないので,点数が伸び悩んでいましたね。
問題
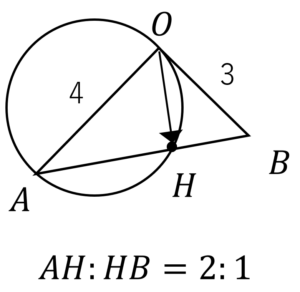
\(OA=4,OB=3\)である三角形\(OAB\)において,辺\(AB\)を2:1に内分する点を\(H\)とすると,点\(H\)は線分\(OA\)を直径とする円周上にあるとき,以下の問いに答えなさい。
(1) \(\overrightarrow{OH}\)を\(\overrightarrow{OA},\overrightarrow{OB}\)を用いて表しなさい。また,\(\overrightarrow{OA}・\overrightarrow{OB}\),\(\cos \angle AOB\)を求めなさい。
(2) 辺\(OA\)の中点を\(C\),辺\(OB\)を2:1に内分する点を\(D\)とし,線分\(CD\)と線分\(OH\)の交点をEとするとき,\(\overrightarrow{OE}\)を\(\overrightarrow{OA},\overrightarrow{OB}\)を用いて表しなさい。
(3) (2)のとき,実数\(x,y\)に対して
\(\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OE}\)
で定まる点\(P\)を考える。
\(2x+y=1,x\geq 0,y \geq 0\)を満たすとき,点\(P\)の存在する範囲は\(線分AE,線分AH,線分CE,線分CH\) のうちどれか?また,その線分の長さはいくらになるか?
(4) \(x \geq 0,y \geq 0,1 \leq x+y \leq 2\)を満たすとき,点\(P\)の存在する範囲の面積を\(S\)とすると,\(S\)は三角形\(OAB\)の面積の何倍であるか?
問題解答
(1)解答
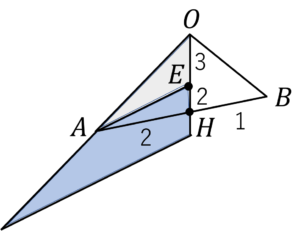
図より,点\(H\)は,辺\(AB\)を2:1に内分するので,
\(\overrightarrow{OH}=\frac{1・\overrightarrow{OA}+2・\overrightarrow{OB}}{3}=\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}\)
点\(H\)は線分\(OA\)を直径とする円周上にあるから,図で書くと,
線分\(OH\)と線分\(AB\)は直角であることがわかります。(∵円周角の定理)
\(\overrightarrow{OH}・\overrightarrow{AB}=0\)
が成立します。この式を式変形して,\(\overrightarrow{OA}・\overrightarrow{OB}\)を求めます。
\(\underbrace{\frac{1}{3}(\overrightarrow{OA}+2\overrightarrow{OB})}_{\overrightarrow{OH}}・\underbrace{(\overrightarrow{OB}-\overrightarrow{OA})}_{\overrightarrow{AB}}=0\)
\(-|\overrightarrow{OA}|^2+2|\overrightarrow{OB}|^2-\overrightarrow{OA}・\overrightarrow{OB}=0\)
\(\overrightarrow{OA}・\overrightarrow{OB}=2・3^2-4^2\)
\(\overrightarrow{OA}・\overrightarrow{OB}=2\)
また,\(\cos \angle AOB\)は,
\(\cos \angle AOB=\frac{\overrightarrow{OA}・\overrightarrow{OB}}{|\overrightarrow{OA}||\overrightarrow{OB}|}=\frac{2}{4・3}\)
\(\cos \angle AOB=\frac{1}{6}\)
(2)解答
\(\overrightarrow{OE}\)を求める前に,\(\overrightarrow{OC},\overrightarrow{OD}\)を求めましょう。
点\(C\)は辺\(OA\)の中点なので,
\(\overrightarrow{OC}=\frac{1}{2}\overrightarrow{OA}\)
点\(D\)は辺\(OB\)を2:1に内分するので,
\(\overrightarrow{OD}=\frac{2}{3}\overrightarrow{OB}\)
\(\overrightarrow{OE}\)は図のように表されるので,
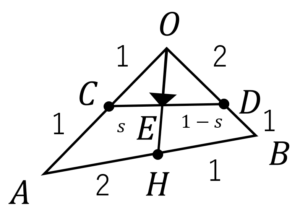
次の2式が成立します。
\(\overrightarrow{OE}=k\overrightarrow{OH}=\frac{1}{3}k\overrightarrow{OA}+\frac{2}{3}k\overrightarrow{OB}\tag{1}\)
\(\overrightarrow{OE}=(1-s) \overrightarrow{OC}+s\overrightarrow{OD}=\frac{1-s}{2}\overrightarrow{OA}+\frac{2}{3}s\overrightarrow{OB}\tag{2}\)
式(1)=式(2)から,係数比較をすると,
\(\frac{1}{3}k=\frac{1-s}{2}\tag{3}\)
\(\frac{2}{3}k=\frac{2}{3}s\tag{4}\)
式(3),式(4)の連立方程式を解くと,\(k,s\)は
\(k=s=\frac{3}{5}\)
となるので,求めた\(k\)を式(1)に代入すると,\(\overrightarrow{OE}\)は,
\(\overrightarrow{OE}=\frac{1}{5}\overrightarrow{OA}+\frac{2}{5}\overrightarrow{OB}\)
となります。
(3)解答
\(\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OE}\)
を少し式変形して,
\(\overrightarrow{OP}=2x\underbrace{\frac{1}{2}\overrightarrow{OA}}_{\overrightarrow{OC}}+y\overrightarrow{OE}\)
としましょう。
すると,\(2x+y=1\)より,点\(P\)は線分\(CE\)上に存在することがわかります。
また,線分\(CE\)の長さは,\(|\overrightarrow{CE}|\)で表されるので,\(|\overrightarrow{CE}|\)を計算すればいいことがわかります。
\(|\overrightarrow{CE}|=|\overrightarrow{OC}-\overrightarrow{OE}|=|\frac{1}{2}\overrightarrow{OA}-(\frac{1}{5}\overrightarrow{OA}+\frac{2}{5}\overrightarrow{OB})|\)
\(=|\frac{3}{10}\overrightarrow{OA}-\frac{2}{5}\overrightarrow{OB}|\)
\(=\sqrt{(\frac{3}{10}\overrightarrow{OA}-\frac{2}{5}\overrightarrow{OB})^2}\)
\(=\sqrt{\frac{9}{100}|\overrightarrow{OA}|^2+\frac{16}{100}|\overrightarrow{OB}|^2-4\frac{3・2}{2・10・5}\overrightarrow{OA}・\overrightarrow{OB}}\)
\(=\sqrt{\frac{9}{100}4^2+\frac{16}{100}3^2-\frac{24}{100}2}\)
\(=\sqrt{\frac{240}{100}}=\sqrt{\frac{60}{25}}\)
\(=\frac{2\sqrt{15}}{5}\)
(4)解答
図を書くと,
図から,
\(S=3\triangle OAE=3\frac{3}{5}\triangle OAH=3\frac{3}{5}\frac{2}{3}\triangle OAB=\frac{6}{5}\triangle OAB \)
まとめ
円周角の定理
「円周角は中心角の1/2」⇒ex)中心角が180°なら円周角は90°
最後に
平面ベクトルは,図を書ければ余裕で解ける。