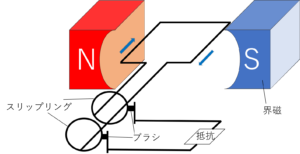
今日は,同期電動機の中でも簡単な永久磁石同期電動機の解析方法とその概略について述べてゆく。さぁ,ゆくぞ!
永久磁石同期電動機の構造を詳しく見るためには,大学の電気回路学という学問に加え,高校数学Ⅲまでを網羅する必要があります。
また,「ベクトル解析学」のベクトル演算などの知識も使います。
この記事を読むメリット
☑永久磁石同期電動機の特性を理解しよう!
☑三相二相変換(\(\alpha \beta\)-dq変換)について学べる
同期電動機(同期機)とは?構造について
皆さんは,直流機,交流機を知っていますか?
電気機器は,直流機と交流機のどちらかに分類されています。
詳しくは,下記のサイトが詳しく書かれていましたのでご紹介します。
同期電動機(同期機)は,交流機の一種で,回転磁界と同期して回転するので,同期機と呼ばれています。
同期機に対して,回転磁界と同期せずに回転しない電気機器は,誘導機と呼ばれています。
今回ご紹介するのは,同期機の中でも同期電動機(同期モータ)と呼ばれる機器です。(電動機は,電気⇒回転力に変換,発電機は,回転力⇒電気に変換)
| 直流機 | 直流電動機 | |
| 直流発電機 | ||
| 交流機 | 同期機 | 同期電動機 |
| 同期発電機 | ||
| 誘導機 | 誘導電動機 | |
| 誘導発電機 |
同期電動機の図を見ていきましょう。
同期電動機の基本構造は,交流機と大差ありません。
今回ご紹介する機器は,永久磁石同期電動機で,通常の同期電動機の界磁(界磁巻線+界磁鉄心)を永久磁石に置き換えた物になります。
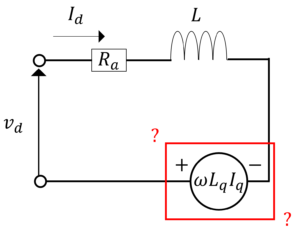
このことを踏まえて,永久磁石同期電動機の等価回路を描くと
このようになります。
実際の同期電動機は電流が流れる導線を3つに増やして,三相同期電動機として使われます。
->
すると、回路解析を行う際に等価回路が3つに増えて厄介です。
そこで,\(\alpha \beta \)-dq変換(三相二相変換)を使います。
三相同期電動機の解析\(\alpha \beta\)―dq変換
永久磁石同期電動機の等価回路
結論から言うと,永久磁石同期電動機の等価回路は以下の通りになります。
図1.d軸等価回路(左)とq軸等価回路(右)
d軸電流\(i_d\)とq軸電流\(i_q\)および電機子電流\(I_a\)と電流位相\(\beta\)の関係は,
$$\left \{
\begin{array}{ccc}
i_d=-I_a \sin \beta \\
i_q=I_a \cos \beta
\end{array}
\right.$$
となります。更に,d軸端子電圧\(v_d\),q軸端子電圧\(v_q\)の回路方程式は,
$$\left \{
\begin{array}{ccc}
v_d=R_ai_d+L_d\frac{di_d}{dt}-\omega L_qi_q\\
v_q=R_ai_q+L_q\frac{di_q}{dt}+\omega L_di_d+\omega \psi_a
\end{array}
\right.$$
\(R_a\):電機子巻線抵抗,\(L_d\):d軸インダクタンス,\(L_q\):q軸インダクタンス
\(psi_a\):磁石による電機子巻線鎖交磁束
発生するトルク\(T\)は,
$$T=p[\phi_m i_q+(L_q-L_d)i_di_q]=p[\psi_a I_a \cos \beta+\frac{1}{2}(L_q-L_d)I_a^2 \sin 2\beta]$$
で与えられます。
永久磁石同期電動機は,三相ですが,等価回路はd軸とq軸の2つしか現れません。
しかも,赤枠で囲まれている素子が謎ですよね?
今から等価回路の導出をしていきます。
電流,電圧ベクトルの定義
まず,電流ベクトル\(i_{\alpha \beta}\),電圧ベクトル\(i_{\alpha \beta}\)を定義します。
三相電流が作る磁界をベクトルで表しましょう。
すると,
このようになります。
三相同期電動機の3つの導線に流れる電流をそれぞれ,\(i_u,i_v,i_w\)とし,単位ベクトルをそれぞれ,\(1,e^{-j\frac{2}{3}\pi},e^{-j\frac{4}{3}\pi}\)と置き,3つの電流を合成した電流を\(i_{\alpha \beta}\)とすると,
\(i_{\alpha \beta}=\sqrt{\frac{2}{3}}[i_u・1+i_v・e^{-j\frac{2}{3}\pi}+i_w・e^{-\frac{4}{3}\pi}]\)
\(\alpha \beta\)軸は,次のようにとります。
となります。同様に電圧ベクトル\(v_{\alpha \beta}\)は,
\(v_{\alpha \beta}=\sqrt{\frac{2}{3}}[ v_u・1+v_v・e^{-j\frac{2}{3}\pi}+v_w・e^{-\frac{4}{3}\pi}]\)
と書けます。\(\sqrt{\frac{2}{3}}\)は,計算を簡略化する為の係数です。
三相同期電動機における消費電力\(p\)は,
\(p=v_ui_u+v_vi_v+v_wi_w\)
と書けますが,先ほど定義した電流ベクトル\(i_{\alpha \beta}\)と電圧ベクトル\(v_{\alpha \beta}\)を用いて表すこともできます。
\(p=v_{\alpha \beta}・i_{\alpha \beta}=\frac{2}{3}[i_u・1+i_v・e^{-j\frac{2}{3}\pi}+i_w・e^{-\frac{4}{3}\pi}]・[i_u・1+i_v・e^{-j\frac{2}{3}\pi}+i_w・e^{-\frac{4}{3}\pi}]\)
同じベクトル同士の内積は,\(|1||1|\cos 0=1\)
三相電流の隣り合うベクトル同士の内積は,\(|1||1|\cos \frac{2}{3}\pi=-\frac{1}{2}\)
となるので,電力\(p\)は,
\(p=\frac{2}{3}[v_u(i_u-\frac{1}{2}i_v-\frac{1}{2}i_w)+ v_v(i_v-\frac{1}{2}i_w-\frac{1}{2}i_u)+ v_w(i_w-\frac{1}{2}i_u-\frac{1}{2}i_v)]\)
\(p=\frac{2}{3}[ V \cos (\omega t)( I \cos (\omega t)-\frac{1}{2} I \cos (\omega t-\frac{2}{3}\pi)-\frac{1}{2} I \cos (\omega t-\frac{4}{3}\pi))\)
\(+ V \cos (\omega t-\frac{2}{3}\pi) (I \cos (\omega t-\frac{2}{3}\pi)-\frac{1}{2} I \cos (\omega t-\frac{2}{3}\pi)-\frac{1}{2} I \cos (\omega t-\frac{4}{3}\pi))\)
\(+ V \cos (\omega t-\frac{4}{3}\pi) (i_w-\frac{1}{2} I \cos (\omega t-\frac{2}{3}\pi)-\frac{1}{2} I \cos (\omega t-\frac{4}{3}\pi))]\)
\(p=\frac{2}{3}[ V \cos (\omega t)( I \cos (\omega t)-I \cos (\omega t) \underbrace{\cos (\frac{2}{3}\pi)}_{-\frac{1}{2}})\)
\(+ V \cos (\omega t-\frac{2}{3}\pi) (I \cos (\omega t-\frac{2}{3}\pi)- \cos (\omega t-\frac{2}{3}\pi) \underbrace{\cos (\frac{2}{3}\pi)}_{-\frac{1}{2}})\)
\(+ V \cos (\omega t-\frac{4}{3}\pi) (i_w-\cos (\omega t-\frac{4}{3}\pi) \underbrace{\cos (\frac{2}{3}\pi)}_{-\frac{1}{2}} )]\)
\(p=\frac{2}{3}\frac{3}{2}[ v_ui_u+v_vi_v+v_wi_w]= v_ui_u+v_vi_v+v_wi_w \)
となります。
よって,電流ベクトル\(i_{\alpha \beta}\),電圧ベクトル\(v_{\alpha \beta}\)を次のように定義して良いということがわかりました。
ちなみに,電流ベクトル\(i_{\alpha \beta}\),電圧ベクトル\(v_{\alpha \beta}\)は
フェーザ表示を使うと,もっと簡単に表すことができます。
\(i_{\alpha \beta}=\sqrt{\frac{2}{3}} \sqrt{2}I_m[\cos (\omega t)+\cos (\omega t-\frac{2}{3}\pi)e^{-j\frac{2}{3}\pi}+\cos (\omega t-\frac{4}{3}\pi)e^{-j\frac{4}{3}\pi}\)
\(i_{\alpha \beta}=\sqrt{3}I_m \cos (\omega t)=\sqrt{3}\dot{I}\)
同様に電圧ベクトルも
\(v_{\alpha \beta}=\sqrt{3}V_m \cos (\omega t)=\sqrt{3}\dot{V}\)
$$i_{\alpha \beta}=\sqrt{3}\dot{I}=\sqrt{3}I_m e^{j\omega t}$$
$$v_{\alpha \beta}=\sqrt{3}\dot{V}=\sqrt{3}V_m e^{j\omega t}$$
$$p=v_{\alpha \beta}・i_{\alpha \beta}$$
dq軸(回転座標)の定義
先ほど,\(\alpha \beta\)軸を定義しました。
次は,dq座標を定義しましょう。

\(\alpha \beta\)軸は静止した座標系でしたが,dq軸は角速度\(\omega \)で反時計回りに角速度\(\omega\)で回転する座標です。


ここで,dq座標上の電流,電圧を新たに\(i_{dq}\),\(v_{dq}\)と定義すると,電流\(\)
\(i_{dq}=e^{-j\omega t} i_{\alpha \beta}=\sqrt{3}I_m\)
\(v_{dq}=e^{-j\omega t}v_{\alpha \beta}=\sqrt{3}V_m\)
dq座標(回転座標)では,電流\(i_{dq}\)と電圧\(v_{dq}\)は向きと大きさが一定になります。
ここで,電圧\(v_{\alpha \beta}\)の回路方程式は,電機子巻線抵抗\(R_a\),インダクタンス\(L\),出力端子に生じる電圧\(\psi_{\alpha \beta}\),
\(v_{\alpha \beta}=R_a i_{\alpha \beta}+\frac{d}{dt}(Li_{\alpha \beta}+e_{\alpha \beta})\)
\(e^{j\omega t}v_{dq}= R_a e^{j\omega t} i_{dq}+\frac{d}{dt}(L e^{j\omega t} i_{dq})+ e^{j\omega t} e_{dq}\)
\( e^{j\omega t}v_{dq}= R_a e^{j\omega t} i_{dq}+ e^{j\omega t}\frac{d}{dt}(L i_{dq})+j \omega e^{j\omega t} L i_{dq}+ e^{j\omega t} e_{dq}\)
\(v_{dq}= R_a i_{dq}+ \frac{d}{dt}(L i_{dq})+j \omega L i_{dq}+ e_{dq}\)
ここで,磁界は,q軸方向に発生しているので,\(v_{dq}=i_d+ji_q\),\(e_{dq}=j\omega \psi_a\)が成立するので,
\( v_d+jv_q = R_a (i_d+ji_q)+ \frac{d}{dt}(L i_d+jLi_q)+j \omega L(i_d+ji_q)+ j\omega \psi_a\)
\( v_d+jv_q = R_a i_d+jR_ai_q+ L_d \frac{di_d}{dt}+jL_q\frac{di_q}{dt}+j \omega L_di_d-\omega L_q i_q+ j\omega \psi_a\)
よって,d軸端子電圧\(v_d\),q軸端子電圧\(v_q\)は,
\(\left \{
\begin{array}{ccc}v_d=R_a i_d +L_d\frac{di_d}{dt}-\omega L_q i_q \\
v_q=R_ai_q+L_q\frac{di_q}{dt}+\omega L_di_d+\omega \psi_a
\end{array}
\right.\)
次に,モータの発生トルク\(T_M\)を求めます。トルク\(T_M\)は,モータの電力\(p_M\)と角速度\(\omega\)を用いて,
$$p_M=\omega T_M$$
で表すことができましたので,電力\(p\)を求めて,モータの発生トルク\(T_M\)を求めます。
トルク\(T\)を求める
まず,電力\(p\)について,
\(p=v_{dq}・i_{dq}=v_{d}i_{d}+v_{d}i_{q}\)
\(p=[R_a i_d +L_d\frac{di_d}{dt}-\omega L_qi_q]i_d+[R_ai_q+L_q\frac{di_q}{dt}+\omega L_di_d+\omega \psi_a]i_q
\)
\(p=[R_a i_d^2 +L_d i_d \frac{di_d}{dt}-\omega^2 L_q i_qi_d+R_ai_q^2+\omega L_qi_q\frac{di_q}{dt}+\omega L_di_di_q+\omega \psi_a i_q \)
よって,電力\(p\)は,
\(p= \underbrace{R_a(i_d^2+i_q^2)}_{銅損}+\frac{d}{dt}\underbrace{(\frac{1}{2}L_di_d^2+L_qi_q^2)}_{磁気エネルギー}+\underbrace{\omega \psi_a i_q-(L_q-L_d)i_di_q}_{出力p_M}\)
電力\(p\)の第一項は銅損,第二項は鉄損,第三項は出力\(p_M\)より,発生トルク\(T_M\)は,
\(T_M=\frac{p_M}{\omega}=\psi_a i_q-(L_q-L_d)i_di_q \)
更に,トルク\(T_M\)を電機子電流\(I_a\)と電流位相\(\beta \)で表すと,
\(T_M=\psi_a I_a \cos \beta+(L_q-L_d)I_a^2 \cos \beta \sin \beta\)
ここで,極対数\(p\)を考慮すると,発生トルク\(T\)は,
\(T_M=p[\psi_a I_a \cos \beta+\frac{1}{2}(L_q-L_d)I_a^2 \sin 2\beta]\)
となります。
突極形同期電動機,円筒形同期電動機の違い
同期電動機は,回転子の構造によって,突極形同期電動機,円筒形同期電動機と分類されます。
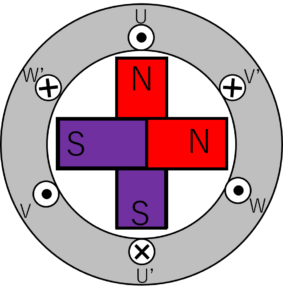
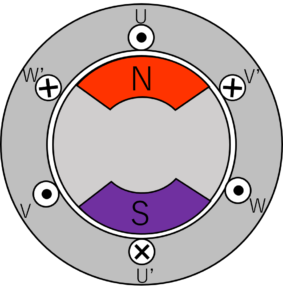
図2.突極形同期電動機(左)と円筒形同期電動機(右)
ここで,突極形同期電動機と円筒形同期電動機についての発生トルク\(T_M\)について考えてみます。
円筒形同期電動機は対称性から,\(L_q=L_d\)が成立するので,
$$T_M=p\psi_a i_a \cos \beta$$
となります。\(\psi_a\)は電機子電流\(i_a\)に依存しないので,円筒形同期電動機の発生トルク\(T_M\)は,電機子電流\(i_a\)に比例して増加することがわかります。
円筒形同期電動機に対して,突極形同期電動機は非対称で\(L_q≠L_d\)より,
$$T_M=p[\psi_a i_a \cos \beta +\frac{1}{2}(L_q-L_d)i_a^2 \sin 2\beta]$$
となり,発生トルク\(T_M\)は,電機子電流\(I_a\)の二次関数になります。
まとめ
・同期電動機(同期機)は,交流機(交流で動作)の一種
・同期電動機には,突極形同期電動機と円筒形同期電動機がある
・三相同期電動機の等価回路は,
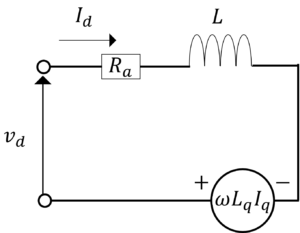
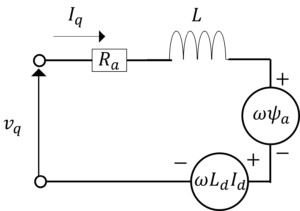
・上の等価回路から三相同期電動機の回路方程式は,
$$\left \{v_d=R_a i_d +L_d\frac{di_d}{dt}-\omega L_q i_q \\
v_q=R_ai_q+L_q\frac{di_q}{dt}+\omega L_di_d+\omega \psi_a
\right.$$
・突極形同期電動機の発生トルク\(T_M\)は,
$$T_M=p[\psi_a i_a \cos \beta+\frac{1}{2}(L_q-L_d) i_a^2 \sin 2\beta]$$
円筒形同期電動機の発生トルク\(T_M\)は,
$$T_M=p\psi_a i_a \cos \beta $$
最後に
永久磁石同期電動機は,電磁石(界磁巻線+界磁鉄心)を用いないので,界磁巻線電流\(i_f\)を考える必要がないです。なので,卒業研究で研究の対象になりやすいです。
卒業研究を何にしようか悩み中。